Polynomial data compression
P. Aubert, T. Vuillaume, G. Maurin, J. Jacquemier, G. Lamanna, N. Emad (Laboratoire d’Annecy de Physique des Particules, Université Savoie Mont-Blanc, CNRS/IN2P3; Laboratoire d’informatique Parallélisme Réseaux Algorithmes Distribués, UFR des Sciences; Maison de la Simulation, Université de Versailles, France) - ASTERICS Work Package 3
The increasing volumes of data generated by large research infrastructures impose great technical constraints on the transfer, storage, processing, dissemination and preservation of these data. The Cherenkov Telescope Array (CTA) for example will generate hundreds of PB of raw data per year. Compression of data can help ease these constraints. However, lossy compression can be an issue for physical data that should stay unaltered. Lossless compression algorithms such as LZMA or GZIP providing the best compression ratios often show compression speeds incompatible with the quantity of data to compress and with the infrastructures data flows.
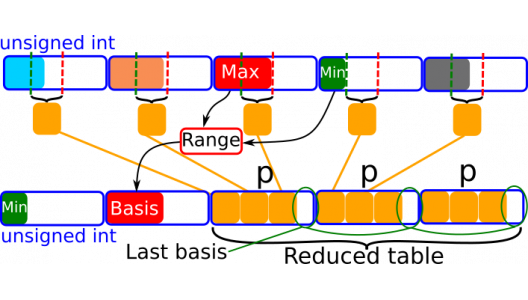
In many cases, the raw data are unsigned integers coming from digitalized signals and presenting a noise close to white noise with a Gaussian distribution and a signal following another distribution. However, these distributions of values do not often cover the distribution of values covered by one unsigned int (16 or 32 bits).
A compression was developed to leverage these facts to store several values of data into one unsigned int, storing once the data minimal value and the range covered by data values as a basis (see figure).
There are several advantages of this method: it can compress blocks of data independently as opposed as compressing a whole file, and it adapts the compression to the signal to compress and achieves very good compression ratio in very small compression times. Moreover, when combined with other compression methods such as LZMA, we observe that we achieve the same maximal compression ratio as LZMA but significantly faster (19 times in our tests).

 ASTERICS is a project supported by the European Commission Framework Programme Horizon 2020 Research and Innovation action under grant agreement n. 653477
ASTERICS is a project supported by the European Commission Framework Programme Horizon 2020 Research and Innovation action under grant agreement n. 653477